The Necessity of Metaphysics

Metaphysics, root meaning being "what comes after physics", is in the most abstract and broad sense, the study of Existence itself.
What is being offered here is not an argument for any particular system of metaphysics but to point out the necessity of metaphysics itself, as a contrast to all viewpoints that denigrate or deny metaphysics, more specifically the argument presented is that any attempt to do away with metaphysics is necessarily an application of metaphysics in some form itself, and therefore an incoherent argument.

In essence, we cannot do away with Metaphysics as much as we want to, so we should get to work in establishing and advancing Metaphysics.

​​

​

Given the attempts to relegate metaphysics to 'mere subjectivity', Alfred North Whitehead's quote "Every scientific man in order to preserve his reputation has to say he dislikes metaphysics. What he means is he dislikes having his metaphysics criticised" rings true.

​​

​

Godel's Incompleteness Theorems

​

Our argument starts with Godel's Incompleteness Theorems and their subsequent philosophical implications, but it should be noted that the specific way you interpret Godel's Theorems can lead to vastly different results -- this is most clearly seen by the fact, following the publications of his result, Godel's felt that it validated his stance as a Neoplatonist that believed in an objective reality, and yet solipsist and existential positions (read: reality is unknowable) often cite varying interpretations of the Theorems -- so we must first outline what these ideas are carefully before coming to any conclusions from them.

​​

​

Godel constructed a mathematical equivalent to the Liar Paradox: The statement 'this sentence is a lie' is a paradoxical statement, for if it is true that the sentence is a lie, that is a direct contradiction. Here is how he did it, in simple terms.
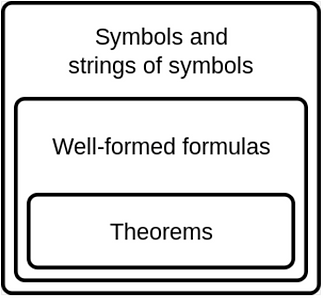
Mathematical expressions derive from axiomatic truths, which are essentially truths we assume to be true for the sake of argument, and their manipulation through rules of deduction. From a given set of axioms, using rules of deduction, we can write theorems that demonstrate a statement as a logical consequence if the axioms are true. Arithmetic as we commonly understand it generally assumes (out of many possible constructions) the Peano Axioms, a concise list defining a small number of primitive symbols and how they relate to each other, allowing us to phrase any expression of arithmetic as a logical consequence of these axioms. These theorems are proofs that can be established for any mathematical expression, for example Bertrand Russell

proved through the use of Peano axioms, the expression 1 + 1 = 2, in Principia Mathematica.

​

​

​

​

​

​

​

​

​

​

​​

​

​

​

​

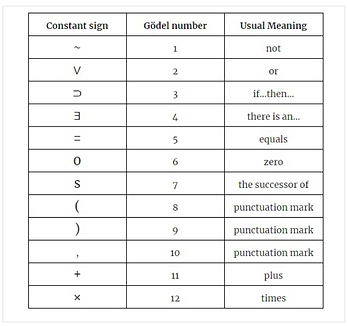
Godel, through the Godel Numbers, assigned every symbol of the Peano system to have a natural number. Using Godel's Numbers, every natural number can be represented as an expression of mathematical symbols converted to natural numbers, and likewise every formula can be represented as a string of Godel Numbers. The twofold brilliance of this is in that it allows us to not only represent mathematical formulas, but also statements about formulas, as strings of Godel Numbers, allowing us to make statements about arithmetic, within arithmetic. This is crucial to Godel's Theorem.

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

(An example of a possible Godel Numbering convention that can be used) Now we know that every provable statement in a formal system must either be an axiom itself, or be derived from the axioms from the application deductive rules. Baked into the definition of a proof S is the structure wherein which a string of mathematical symbols is related via deduction rules to express S as the last statement. Knowing this, we can even give mathematical proofs a Godel number, meaning we can use natural numbers to convey the rules of natural numbers.

​

​

Now for a formal system to be consistent, it cannot prove a statement and its negation, otherwise you can prove every statement in that language. Godel's brilliance came in showing us, mathematically, that every consistent system will have statements that it cannot prove, otherwise the system would be inconsistent. Godel did this by encoding in, with Godel numbers, a statement that informally translates to 'this statement is not provable', which cannot be proven either way. If the statement is provable, it negates itself, a contradiction, therefore the system is not consistent, whereas if it is unprovable, the system is not complete, meaning that there are statements in the language of that formal system can not be proved or disproved within that formal system.

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

It is important to note that Godel's Theorems simply state that any formal system can either be complete, or consistent, but that it cannot be both. With Godel's statement, it was proved that if any sufficiently complex and effectively axiomatised formal system will have statements that it cannot prove, otherwise it will become inconsistent. On its own, despite consistent misinterpretations, Godel's Theorems don't necessarily mean anything, all it does is highlight what was at the time a novel feature of all formal axiomatic systems that fulfil certain criteria (being complex, consistent, and effectively axiomatised).

​

​

That's it.

​

​

A common misconception is to think of Godel's statement as 'true but unprovable', but a truth-value cannot be defined within the system, simply because an 'unprovable formula' can't be represented arithmetically, it is like trying to imagine 'nothing', that's the whole point. Formal systems such as Peano-arithmetic are 'first order languages' that are incapable of proving everything, so second-order languages need to be used to effectively evaluate them. In the context of a first-order formal language such as arithmetic, it makes no sense to describe what is, or isn't, true, as the formal language is only capable of describing the logical consequences of a given set of axioms.

​

​

How, then, does any of this relate to metaphysics?

​

​

Tarski's Undefinability Theorems

​

Godel's work is inherently mathematical in nature, as such you cannot immediately derive any philosophical conclusions from it. On the other hand, Polish logician Alfred Tarski, provides a corollary to the Incompleteness Theorems that relates heavily to 'Truth'.

​

​

If you have any first-order language (such as natural numbers supported by Peano axioms), you can also have an 'interpreted first order language' where by statements in the language (for example 1 + 1 = 2) can be evaluated as 'True' or 'False'. With Godel Numbers, you can 'encode' these statements, such that you can have a list of possible statements (representing formula), and a subset of statements that are evaluated as 'True'. The question is, can you define within the first-order language (arithmetic in this case), a formula that defines all 'True' sentences? Tarski proves that you cannot, by using reductio ad absurdum, which is showing the logical contradiction that this ensures. To express all 'True' statements would require a Godel number, for a number that is not the Godel number of a true sentence, and yet by being a Godel number, it is a true sentence, a clear contradiction, therefore no formula in first-order language can define all 'True' sentences.

​

​

The common informal way of summarising the theorem is succinct in saying 'arithmetical truth cannot be defined in arithmetics', or more broadly that no language can fully represent itself, that to interpret a language in any meaningful sense, it must be done from 'outside' of that language through what Tarski terms 'a metalanguage'. Consequently, this 'metalanguage' must be richer in some sense than the original language, and recursively, this metalanguage too can only be evaluated by yet another meta-metalanguage.

​

​

Metaphysics and Logic

​

Out of the plethora of possible metaphysical conclusions you can derive from this, one of the key relevant conclusions is simply that truth cannot be reduced to any sort of logical or formal system. This much is clear, and is itself a devastating dismantlement of the 'hard' Logical Positivist group, that grew out of the assertion that 'only statements verifiable through direct observation or logical proof are meaningful in terms of conveying truth value, information or factual content'. This entire Philosophy falls apart (and is not considered seriously in Philosophic circles unless in modified forms) precisely because the nature of logical proof is such that it can never be meaningful or provide 'truth value', and that ultimately 'logical proof' itself must stem from the picking of key axioms.

​

​

What I mean to say is, the very structure and nature of Logic and deductive reasoning, and consequently the form and structure of the Scientific Method, is such that it cannot render any picture of 'value' or 'meaning', nor can it define 'truth', none of which is problematic because it isn't trying to. The argument here is not that we should take the

metaphysics already provided for us, but that some form of metaphysical reasoning itself is necessary in order for any form of 'data', 'deduction' or 'logical proof' to have any intelligible use.
The argument that metaphysical claims are not verifiable is itself a supposition that doesn't speak to what we should do about metaphysics, the nature of metaphysics, or even the nature of truth. In essence, it is a meaningless but true observation -- why should they be verifiable?

​

​

One clear example of this is in the choosing of geometric conventions: Euclidean geometry is what use to measure 'real-world things', whereas an infinite number of non-Euclidean geometries exist that are all totally logical and self-consistent, but are not as 'practically useful'. Are these non-Euclidean geometries 'untrue'? The question makes no sense within the context of the geometric convention, the geometry itself is necessitated as logical inferences from starting axioms, and a variety of such axioms can be used for different purposes, therefore none of these geometries are 'true' or 'false', but rather, they can be useful or not, for different purposes. Those purposes themselves, how would they be defined, if not in some metaphysical sense to begin with?

​

​

Scientific theories themselves are frameworks that can encapsulate observable data and attempt to disprove themselves through verifiable hypotheses. Meaning to say, scientific theories framework can never establish and define 'truth'-- it must be done from some sort out of outside perspective, a form of metalanguage, whether that occurs in the form scientific consensus, religious dogma, or some form of 'critical thinking and reasoning', in fact creativity itself can play a crucial role in leading to the synthesis of new scientific explanations -- in all these cases, what takes primacy is not the logical or mathematical process itself, but also the interpretative process that necessitates the logical/ mathematical process.

​

​

Meaning, we are engaging in metaphysics in relationship to science, maths, logic, religion, and just about everything else, all the time, any way, but most of the time we aren't even consciously aware that is indeed what we are doing. Any form of axiomatic presupposition is going to be some form of human-driven thinking or reasoning process, it's not just that metaphysics is necessary in interpreting the use of scientific results, but that our metaphysics structures science itself, in deciding axioms, in outlining the limits of what we can interpret from logical results, and in defining why we use science.

​

​

I would further make the claim that metaphysics, being necessary to science, must have a reciprocal relationship with science. Metaphysical

claims are the root of ethical as well as claims of meaning, use, value, and so in that sense Metaphysics must in some sense inform the structure, nature and direction of scientific innovation. Likewise, though, metaphysics relies on an interpretation of the world, this interpretation itself must be adapted to modern scientific advances and to the ever- growing increase in human knowledge, though as we well know from looking at any sort of arcane belief system, that science generally evolves faster than metaphysics. Returning to Whitehead, even if Metaphysics is constantly changing, constantly wrong, and constantly uncertain, that doesn't mean we shouldn't use Metaphysics -- if it did, by the same token logic we would need to rid ourselves of any sort of established form of assumption or truth in the Sciences as well, a clearly untenable solution.

​

​

Ergo, Metaphysics, and the cultivation and establishment and advance of Metaphysics, is vitally necessary.